NUMERICAL TREATMENT OF TIME-FRACTIONAL ADVECTION DIFFUSION EQUATION VIA B-SPLINE COLLOCATION APPROACH

Abstract

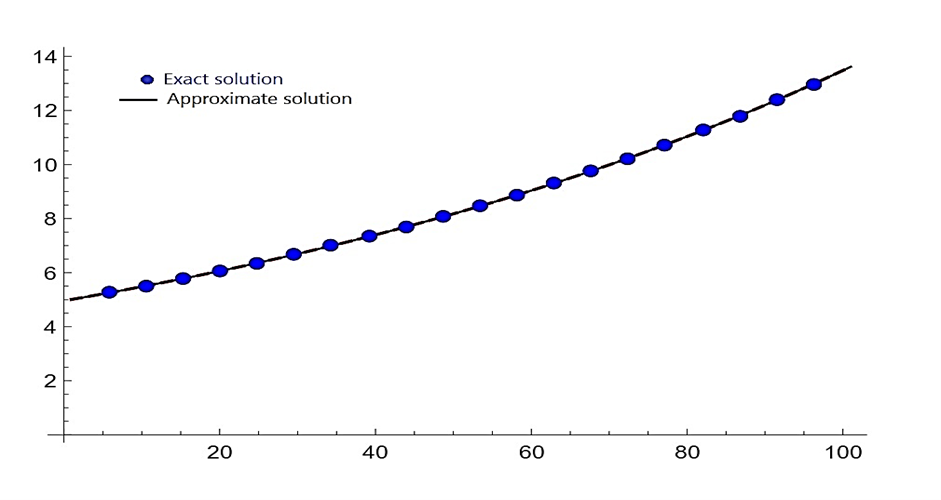
In this work, the approximate solution of the time fractional advection-diffusion equation has been explored. A collection of polynomials in pieces that are smooth and governed by a group of control points comprises the B-spline functions. This study develops a numerical method based on Extended Cubic B-spline (ECBS) functions to solve the time fractional advection-diffusion equation (TFADE). The fractional derivative operator has been used in Caputo-Fabrizio sense, which features a non-singular exponential kernel. The finite difference method (FDM) is applied for temporal discretization while ECBS functions are used to approximate spatial derivatives. A thorough analysis of the method's stability and convergence is presented. Numerical results confirm the effectiveness and precision of the proposed scheme, with computed solutions closely aligning with known analytical solutions.