APPLICATION OF A HYBRID B-SPLINE METHOD FOR THE NUMERICAL ANALYSIS OF TIME-FRACTIONAL DIFFUSION WAVE EQUATION

Sagar Hassan; Muhammad Amin; Saima Mushtaq

doi:10.71146/kjmr515

Authors

Sagar Hassan Faculty of Sciences, The Superior University, Lahore, Pakistan Author
Muhammad Amin Faculty of Sciences, The Superior University, Lahore, Pakistan Author
Saima Mushtaq Faculty of Sciences, The Superior University, Lahore, Pakistan Author

DOI:

https://doi.org/10.71146/kjmr515

Keywords:

Stability, Convergence, Diffusion Wave Equation, Caputo Fabrizio fractional operator, Hybrid Cubic B-Spline (HCBS)

Abstract

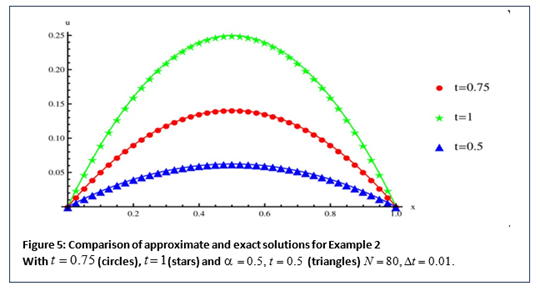
In this article, approximate solutions of Time-Fractional Diffusion Wave Equation has been investigated using a hybrid cubic B-spline technique with finite difference scheme. For the discretization of time fractional derivative Caputo-Fabrizo formula is employed. To get the numerical out comes the Caputo-Fabrizo fractional derivative and a hybrid cubic B-spline strategy is delved. The presented method is proved to be unconditionally stable with a second order convergence. The proposed scheme is validated using some test problems, demonstrating its feasibility and reasonable accuracy. Numerical results show that the applied method is efficient and computationally economic in solving the time-fractional Diffusion Wave Equation.