A COMPARATIVE ANALYSIS OF CHEBFUN AND MATLAB’S BVP4C METHOD FOR SOLVING THE FISHER-KPP EQUATION

Nouman Iftikhar; Zunera Shoukat; Muhammad Zeemam; Saima Mushtaq

doi:10.71146/kjmr276

Authors

Nouman Iftikhar Faculty of Sciences, The Superior University Lahore, Pakistan. Author
Zunera Shoukat Faculty of Sciences, The Superior University Lahore, Pakistan. Author
Muhammad Zeemam Department of Mathematics, Government College University Faisalabad, Pakistan. Author
Saima Mushtaq Faculty of Sciences, The Superior University Lahore, Pakistan. Author

DOI:

https://doi.org/10.71146/kjmr276

Keywords:

Fisher-KPP equation, Chebfun, MATLAB, bvp4c, nonlinear ODE, numerical methods

Abstract

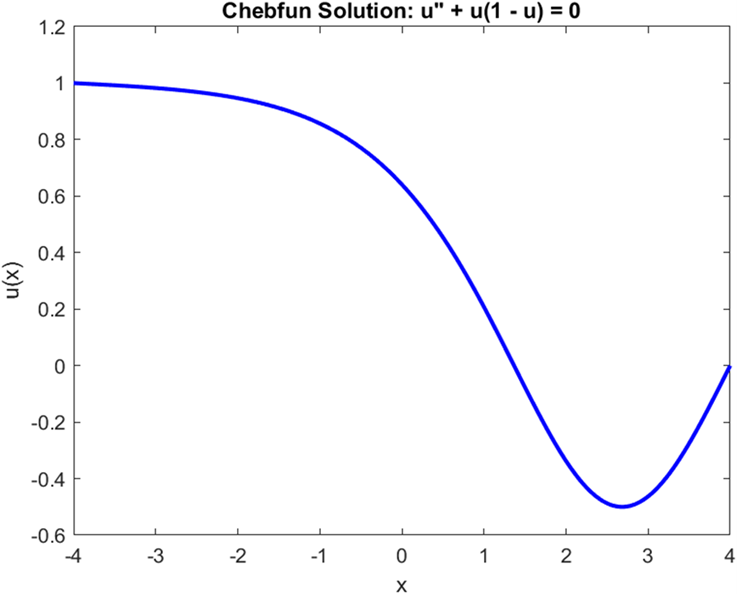
This study investigates numerical solutions to the Fisher-KPP equation, a nonlinear ordinary differential equation (ODE) used in modeling population dynamics and reaction-diffusion processes. We compare two solvers: MATLAB’s bvp4c, a widely-used method for boundary value problems, and Chebfun, which utilizes Chebyshev polynomial approximations for potentially improved accuracy. The performance of both solvers is assessed in terms of accuracy, computational efficiency, and effectiveness for solving the Fisher-KPP equation. The findings highlight the strengths and limitations of each method, offering guidance on selecting the most appropriate solver for nonlinear problems in computational science and engineering.